数学分析I
数学分析之数列的极限
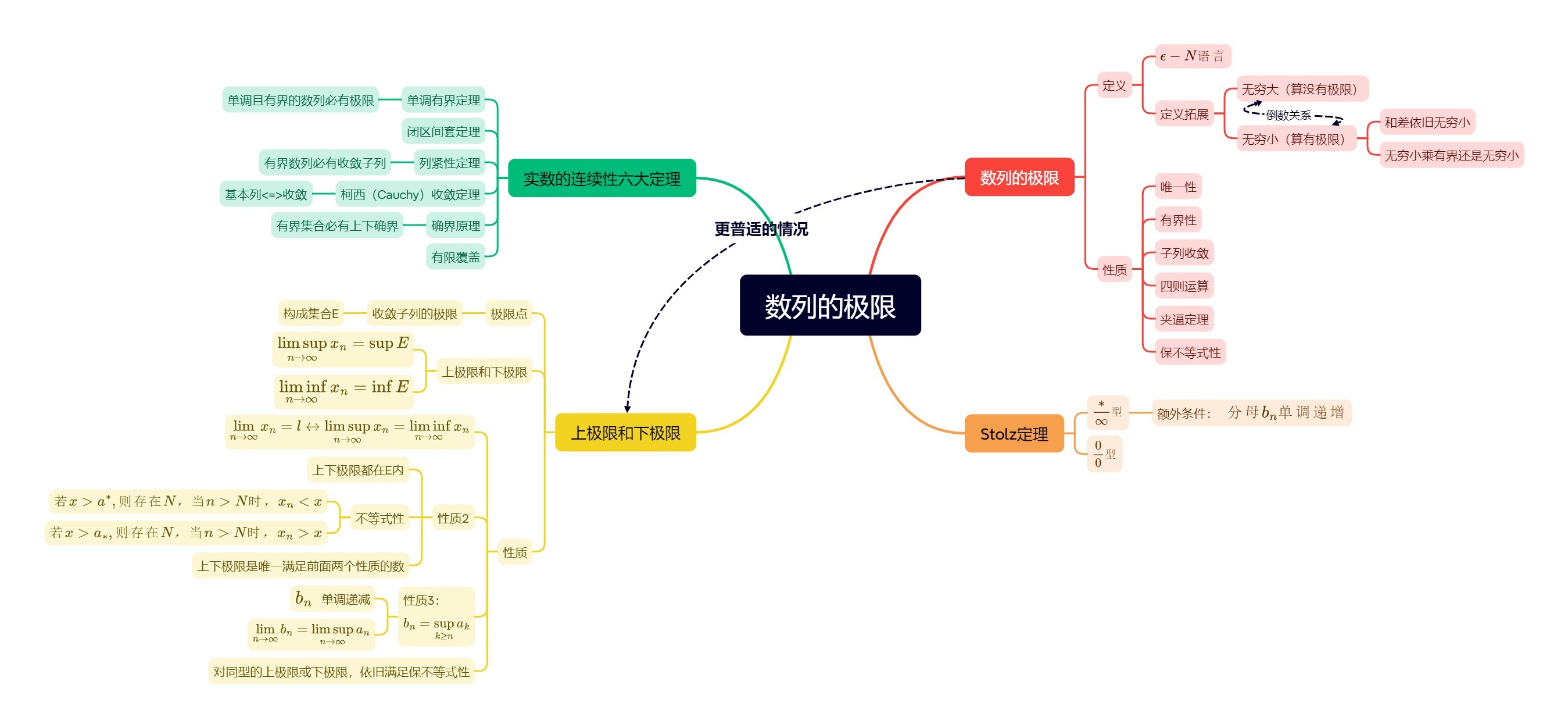
1补充要点
1.证明数列极限的方法
1.定义:(
2.夹逼原理
3.Cauchy收敛
4.单调有界定理
5.子列收敛(所有的数列 or 奇偶数列 等)
6.Stolz定理:
7.计算法:
8.上下极限相同
9.函数极限 + 归结原理
函数的连续性
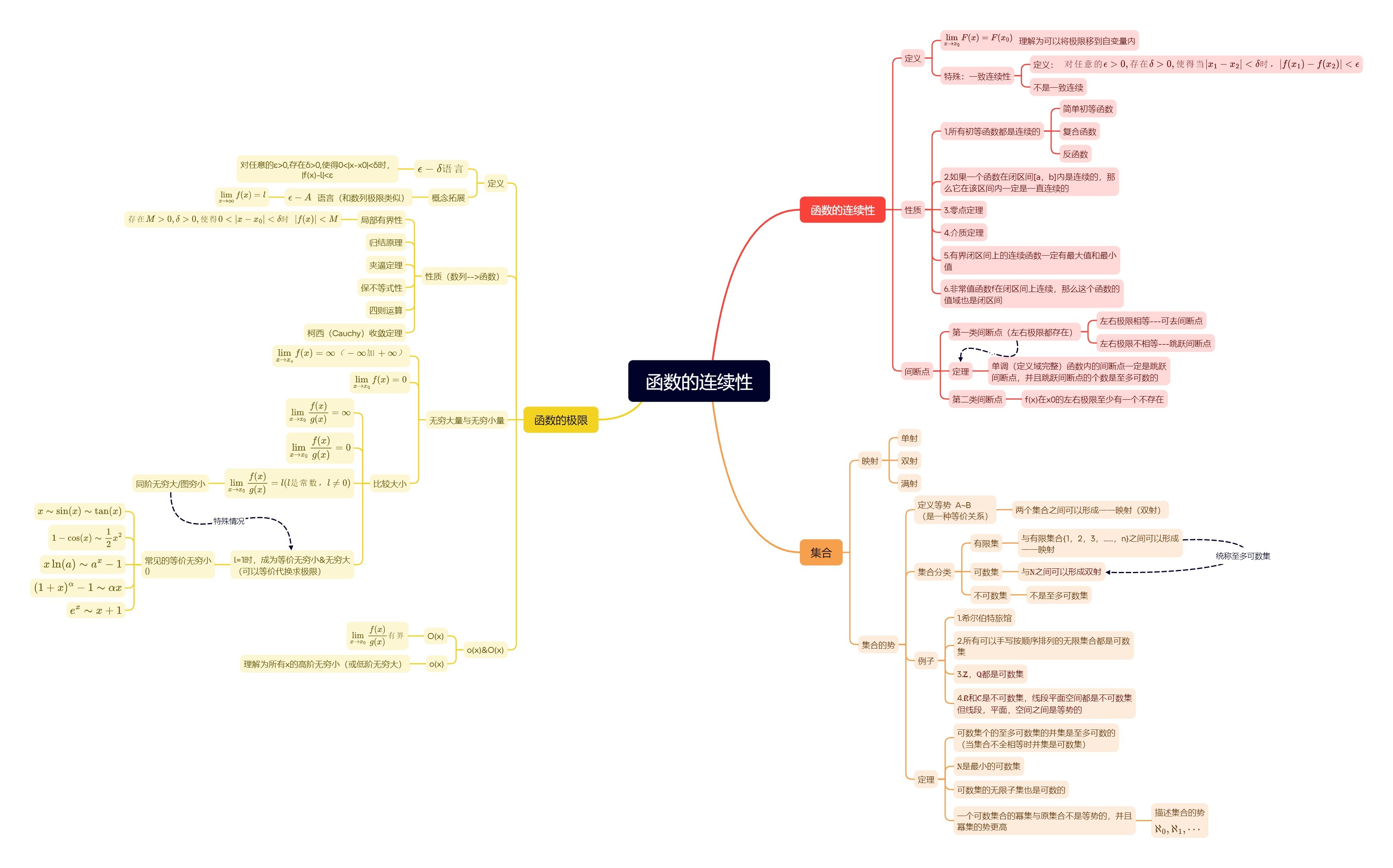
2补充要点
证明函数的极限
1.定义 (
2.归结原理 (用于证明没有极限比较好)
3.函数的连续性(极限等于函数值)
4.等价无穷小(可理解为Taylor展开取一部分)
5.夹逼原理
6.计算法(eg.取e为底数的指数)
7.Cauchy 收敛
8.Taylor 展开:
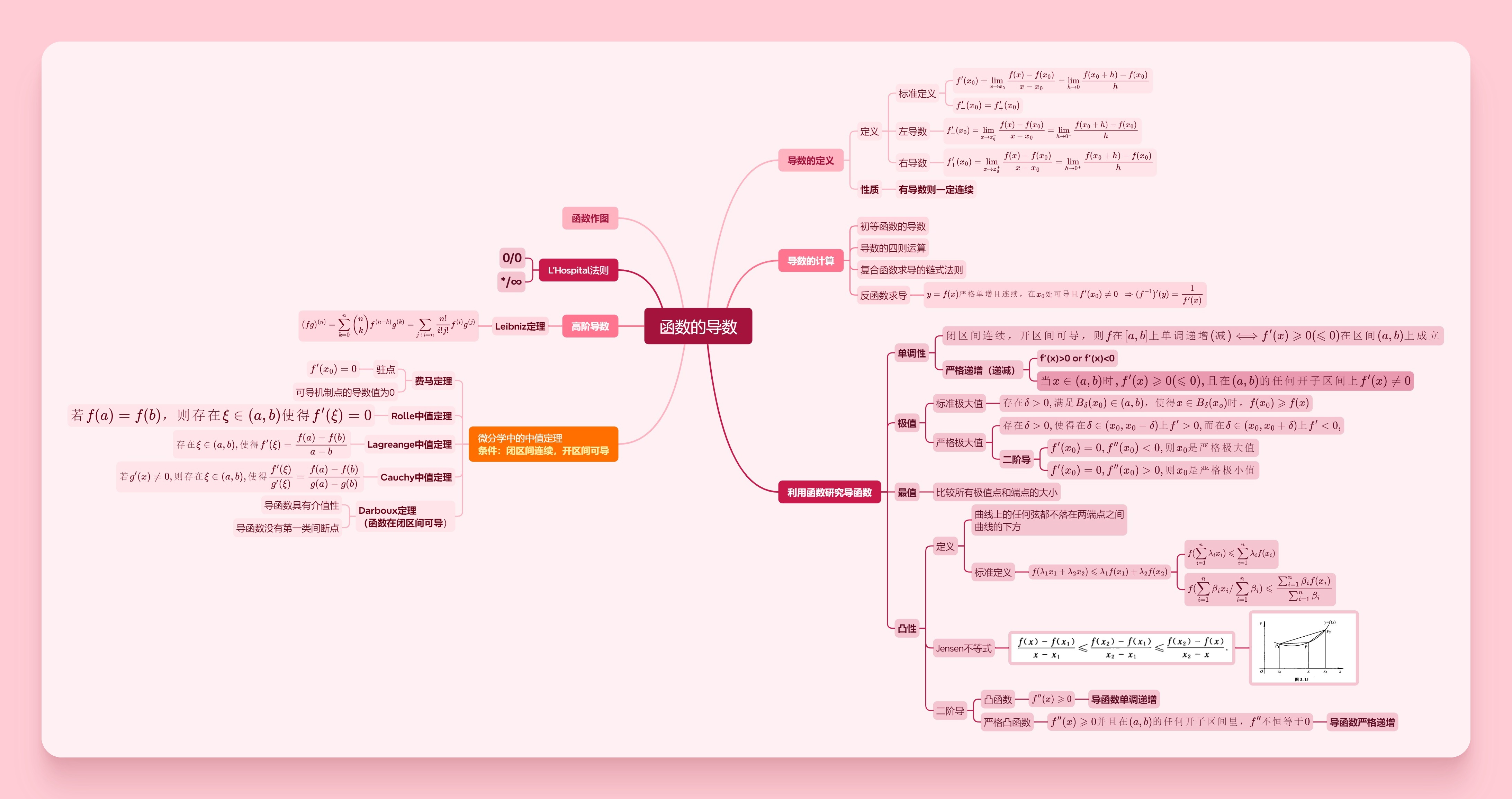
函数的导数
(----😊✌️----)
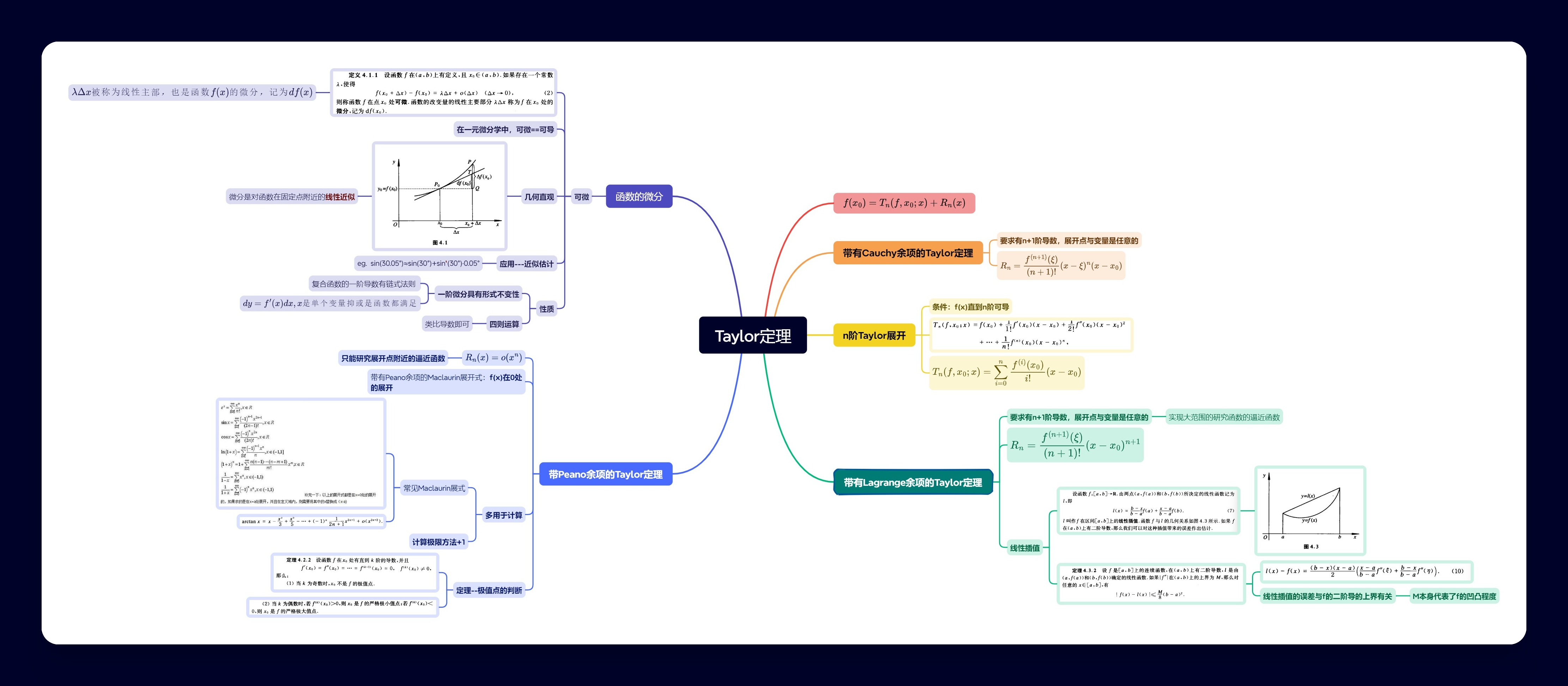
Taylor定理
积分学
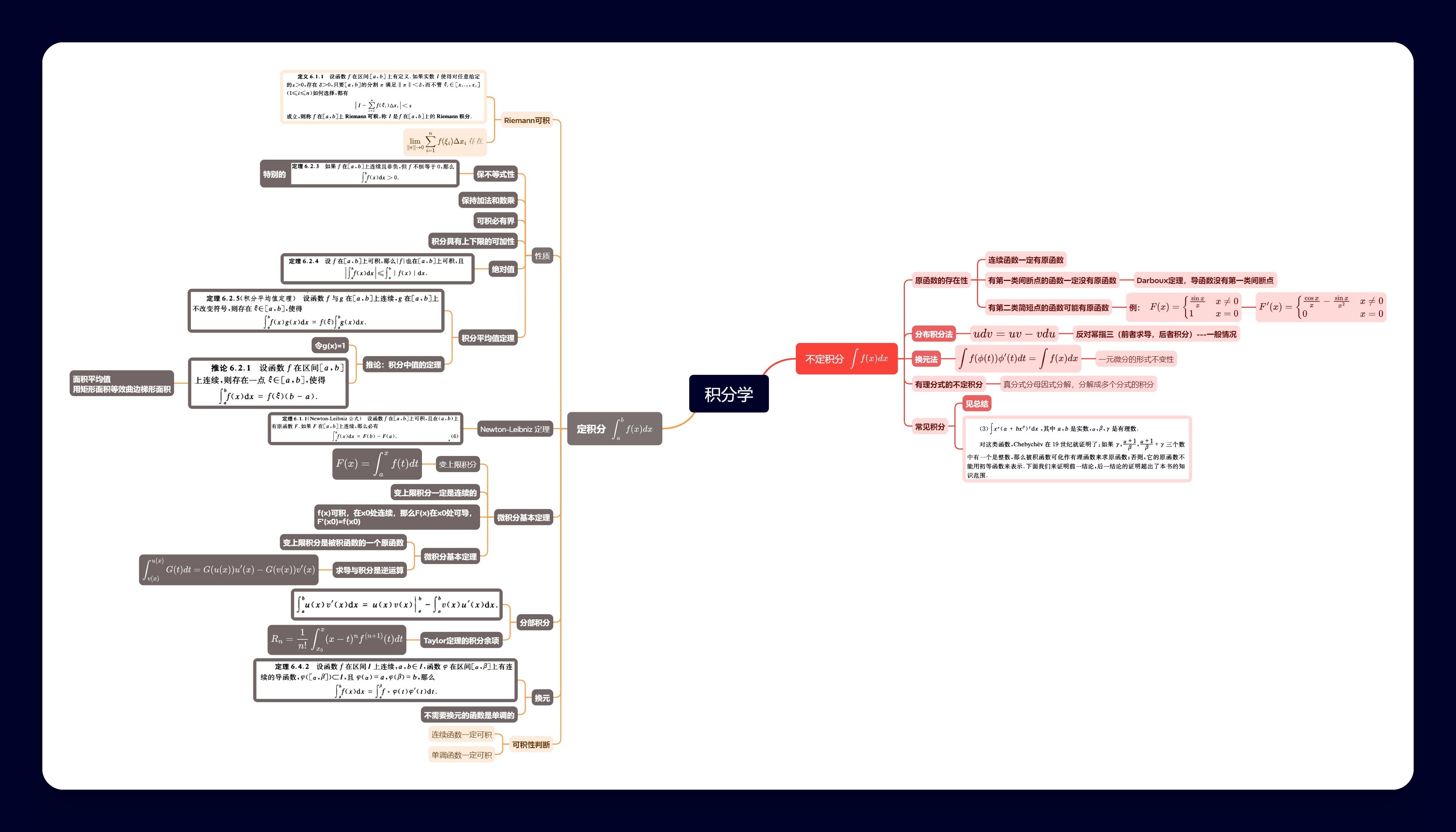
总结
不等式总结
1.Wallis公式 (据说很重要,要记)
定义双阶乘:隔数跳跃乘
tmd 这个代码我鼓捣了将近一个小时一直那\left \{语法,始终渲染不对,知道发现了\begin{cases} 生气了💢💢😡😡,影响我学习🔥😡🔥,在此记录–12月11日
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
Comments
